Плоские кривые — Построение кривых
Решение практических задач по формированию сложных технических контуров наталкивается на такую проблему, как невозможность представления всего контура единственной кривой. Это и породило необходимость конструирования составных кривых (кривых, сформированных из дуг простых).
В технике такие кривые получили название обводов, в математике они более известны как сплайны (spline). Основной характеристикой обвода является гладкость. Под гладкостью понимают число совпавших производных (уравнений стыкующихся кривых) в точках стыка.
Наиболее простой вариант построения составной кривой — из дуг окружностей.
Окружности могут сопрягаться таким образом, что в точках стыка будут располагаться общие касательные. Такой стык соответствует первому порядку гладкости (совпадают только первые производные).
Для построения этого обвода используется идея радиусо-графического сопряжения дуг окружностей. Исходной информацией является точечный ряд (1, 2, 3, …, n) и касательная на одном из концов этого ряда, например, ti (рисунок 1).
Вследствие того, что окружность трехпараметрическая кривая, для её построения кроме точки i нужно определить еще одну, например (i+1) или (i-1). Не нарушая общности рассуждений, рассмотрим вариант с (i+1)-ой точкой (рисунок ниже).
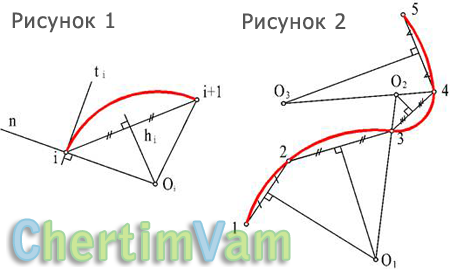
Рисунок 1 — Построение дуги окружности с заданными параметрами
Рисунок 2 — Построение обвода первого порядка гладкости
Графическое решение выглядит следующим образом: через точку i проводится нормаль n. Конечные точки i и (i+1) соединяются хордой. В средней точке хорды строится перпендикуляр h. Пересечение нормали n и перпендикуляра h и определит положение центра искомой окружности. Радиус окружности совпадает с отрезками [o-i] и [o-(i+1)]. Касательная к построенной окружности будет перпендикулярна радиусу, проведенному в (i+1)-ю точку.
Центры соприкасающихся окружностей лежат на одной прямой, проходящей через точку касания. Таким образом, определение центра окружности сопрягающейся с i-той найдется на пересечении линии Оi(i+1) с перпендикуляром к середине хорды (i+1)(i+2) (рисунок 2).
Построение кривых
Ниже приведено построение наиболее наиболее употребительных кривых. На картинке приведена кривая и сохранены все построения. Ниже описан алгоритм построения кривой.
Лекальные кривые
Построение синусоиды
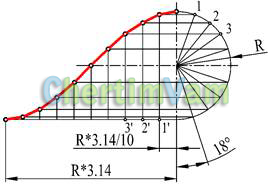
Рисунок 3 — Построение синусоиды
Синусоидой называется плоская кривая, графически изображающая изменение синуса в зависимости от его аргумента (угла). Для построения синусоиды окружность радиуса R делят на произвольное количество равных частей. На горизонтальной прямой откладывают отрезок, равный половине длины окружности (R*3.14), и делят его на такое же число равных частей. Из концов этих отрезков (точки 1′,2′,3′) проводят вертикальные прямые до пересечения с горизонтальными прямыми, исходящими из концов соответствующих радиусов (точки 1,2,3).
Построение циклоиды
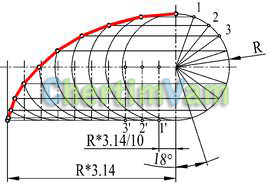
Рисунок 4 — Построение циклоиды
Циклоидой называется кривая, образованная точкой окружности, катящейся без скольжения по прямой линии. Для построения циклоиды окружность радиуса R делят на произвольное количество равных частей. На горизонтальной прямой откладывают отрезок, равный половине длины окружности (R*3.14), и делят его на такое же число равных частей. Из концов этих отрезков (точки 1′,2′,3′) проводят вертикальные прямые до пересечения с горизонтальной осевой линией. Эти точки будут центрами окружностей радиуса R. Пересечения окружностей с соответствующими горизонтальными прямыми, исходящими из концов радиусов (точки 1,2,3), дадут точки циклоиды.
Построение эвольвенты
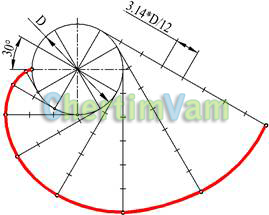
Рисунок 5 — Построение эвольвенты
Эвольвентой окружности называется кривая, которую описывает точка прямой линии, катящейся без скольжения по неподвижной окружности. Окружность диаметра D делят на произвольное число равных частей. Из точек деления проводят касательные к окружности, на которых откладывают соответственно 1, 2, 3 и т.д. части окружности.
Построение параболы
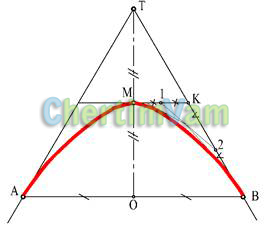
Рисунок 6 — Построение параболы
Параболойназывается, кривая, полученная при пересечении конуса и плоскости, параллельной образующей конуса. При задании параболы граничными точками А и В и точкой пересечения касательных Т кривая строится методом пропорционального деления.
Отрезок АВ делится пополам в точке О, отрезок ОТ – тоже пополам в точке М, отрезок МК — в точке 1, КВ — в точке 2 и т.д.
Построение эллипса
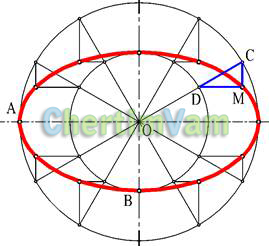
Рисунок 7 — Построение эллипса
Эллипсомназывается кривая, полученная при пересечении конуса и плоскости, пересекающей все образующее конуса.
Эллипс удобнее стоить по его полуосям (большой ОА и малой ОВ).
Для построения эллипса проводятся две соосные окружности радиусами ОВ и ОА Проведение произвольной прямой ОС и дальнейшее построение ”ключа” (треугольника СDМ со сторонами параллельными осям эллипса) позволяет определить положение текущей точки эллипса М.
Геометрические построения
Ниже даны изображения наиболее распространенных видов геометрических построений и описан алгоритм построения.
Касательная к эллипсу
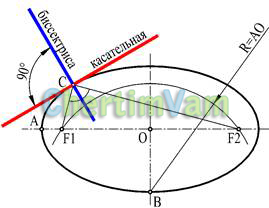
Рисунок 8 — Касательная к эллипсу
Построение касательной к эллипсу (с полуосями ОА и ОВ) в заданной точке С нужно начинать с построения фокусов эллипса, точек F1 и F2.
Построить окружность с центром в точке В и радиусом, равным большой полуоси ОА. В пересечении окружности с горизонтальной осью отметить точки F1 и F2. Построить биссектрису угла F1СF2. Прямая, перпендикулярная биссектрисе и проходящая через точку С, будет касательной к эллипсу в заданной точке.
Построение биссектрисы угла
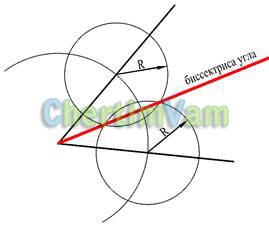
Рисунок 9 — Построение биссектрисы угла
Из вершины угла произвольным радиусом построить дугу окружности. Из точек пересечения дуги окружности со сторонами угла построить равные окружности произвольного радиуса R. Прямая, проходящая через вершину угла и точки пересечения окружностей, — биссектриса угла.
Геометрическое построения сопряжения прямых
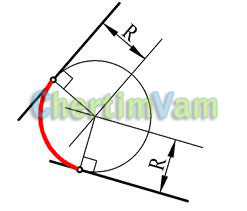
Рисунок 10 — Сопряжение прямых окружностью заданного радиуса R
На расстоянии R от заданных прямых построить вспомогательные прямые, им параллельные. Из точки пересечения вспомогательных прямых построить сопрягающую окружность заданного радиуса R. Отметить точки сопряжения. Они лежат на перпендикулярах, проведенных из центра сопрягающей окружности к заданным прямым.
Построение сопряжения прямой и дуги
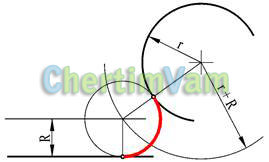
Рисунок 11 — Сопряжение окружностью заданного радиуса R прямой и дуги
На расстоянии R от заданной прямой построить вспомогательную прямую, ей параллельную. Из центра сопрягаемой дуги провести дугу окружности с радиусом r + R. Из точки пересечения построенной дуги и вспомогательной прямой построить сопрягающую окружность. Отметить точки сопряжения.
Построение сопряжения двух окружностей
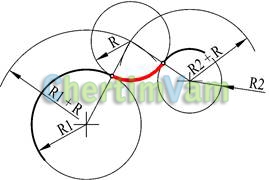
Рисунок 12 — Внешнее сопряжение окружностью с заданным радиусом R двух окружностей с радиусами R1 и R2
Из центров заданных окружностей провести дуги вспомогательных окружностей с радиусами R1+R и R2+R. Из точки пересечения дуг вспомогательных окружностей построить сопрягающую окружность радиуса R. Отметить точки сопряжения. Они лежат на прямых, соединяющих центры окружностей.
Геометрические построения смешанного сопряжения
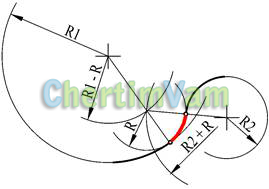
Рисунок 13 — Смешанное сопряжение окружностью с заданным радиусом R двух окружностей с радиусами R1 и R2
Из центров заданных окружностей провести дуги вспомогательных окружностей с радиусами R1-R и R2+R. Из точки пересечения дуг вспомогательных окружностей построить сопрягающую окружность радиуса R. Отметить точки сопряжения. Они лежат на прямых, соединяющих центры окружностей.