Пересечение поверхностей

Из линейной алгебры (многомерной геометрии) хорошо известно, что в расширенном евклидовом пространстве Еn+  размерность пересечения геометрических объектов может быть определена из соотношения

p = m1 + m2 — n,
где p — размерность объекта получаемого в пересечении,
m1 — размерность первого объекта (m1 — поверхности),
m2 — размерность второго объекта (m2 — поверхности),
n — размерность рассматриваемого пространства.

В соответствии с выше приведенной формулой пересечение двух поверхностей (двумерных m1 = m1 = 2)  в трехмерном евклидовом пространстве Е3+ должно привести к появлению одномерного объекта p = 2+2-3=1 — пространственной кривой (p = 1), все точки которой являются общими для обеих поверхностей.

При построении линии пересечения наиболее характерны два случая:
— одна из проекций линии пересечения известна и задача сводится к отысканию недостающих проекций точек по принадлежности одной из поверхностей;
— проекции линии пересечения не известны.

И в том и другом случае задача решается введением дополнительных секущих поверхностей, позволяющих находить точки, принадлежащие одновременно трем геометрическим объектам. В качестве дополнительных поверхностей берутся плоскости, цилиндры и сферы, дающие наиболее простые (заранее известные) линии при пересечении с заданными поверхностями.

Метод секущих плоскостей

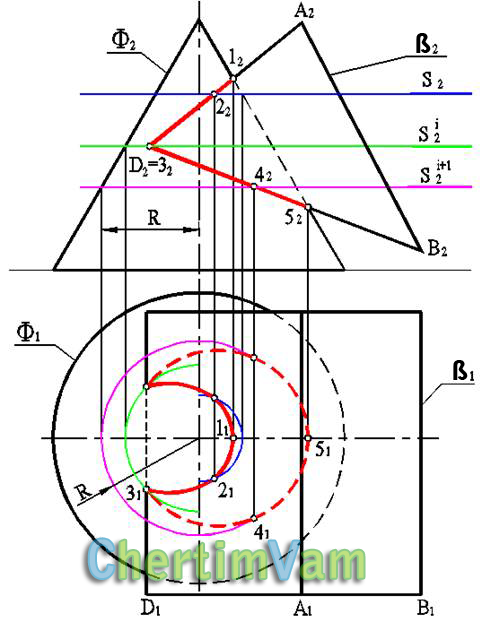
Этот метод применяют для построения линии пересечения поверхностей, позволяющих получать (одновременно) во вводимых секущих плоскостях, графически простые линии (прямые или окружности). Это утверждение может быть проиллюстрировано на примере пересечения призмы ? и конуса Ф (см. рисунок 1, Метод секущих плоскостей).

Здесь в качестве вспомогательных секущих плоскостей выступают горизонтальные плоскости уровня Si. На поверхности конуса (в силу того, что они перпендикулярны оси вращения) эти плоскости выделяют окружности, а на поверхности призмы — параллельные прямые (образующие).

Характерные точки 1, 5 линии пересечения определяют в пересечении фронтальных очерков. Текущие точки линии пересечения  определятся как результат пересечения соответствующих окружностей и прямых в секущих плоскостях Si.

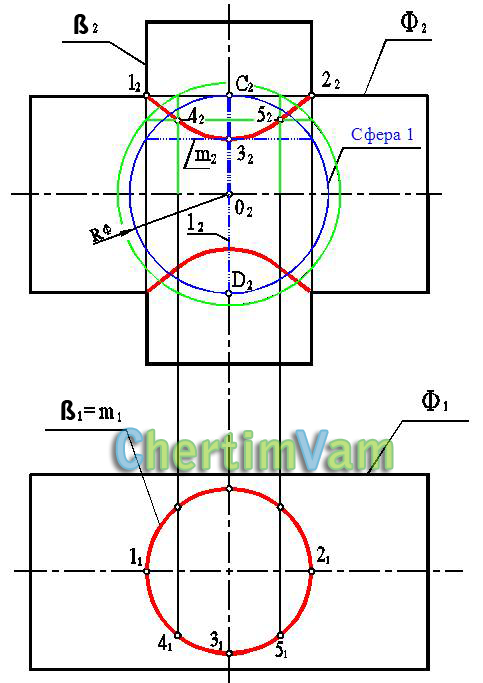
Метод секущих сфер

Линия пересечения двух цилиндров Ф и ? (RФ > R?) может быть определена с помощью метода секущих сфер. Это определяется тем, что рассматриваемые поверхности являются поверхностями вращения и оси вращения пересекаются.

Линия пересечения распадается на две ветви, нижнюю и верхнюю, построение которых аналогично (см. рисунок 2, Метод секущих сфер).

Фронтальные проекции характерных точек линии пересечения 12 и 22 определятся в результате пересечения фронтальных очерков Ф2 и ?2 ,а горизонтальные — определятся по принадлежности этих точек цилиндру ?.

Низшая точка линии пересечения (3)определяется введением сферы RФ, которая пересечет цилиндр Ф по окружности l(фронтальная проекция этой окружности совпадет с фронтальной проекцией оси вращения цилиндра ?).

С цилиндром ? эта же сфера пересечется по окружностиm. Точка  3 и есть результат пересечения окружностей lи m.     Промежуточные точки определятся аналогично, как пересечение окружностей, получающихся в пересечении произвольных сфер RФ < Ri < О212 с цилиндрами Ф и ?. Фронтальные проекции точек линии пересечения определяются как пересечения отрезков прямых, в которые вырождаются окружности, перпендикулярные оси вращения, а горизонтальные проекции находятся по принадлежности одной из поверхностей. В данном случае — поверхности ?.